Ok, now I am more confused. We are using different methods to divide, but which is right?
Quote:
Originally Posted by clevermax  Thanks for the exact formula Samurai! But I think the loss in light is 18.57%. |
I know why you are getting a different result.
Quote:
Originally Posted by clevermax  The full f-stops are here for reference:
1.4142
2
2.8284
4
5.6568
8
11.3137
16
22.6274
32
and so on. |
My numbers were even more accurate, I didn't stop at 4th decimal. I used the following fractions as my f-stops:
2^(0/2) = 2^0 = 1
2^(1/2) = 2^0.5 = 1.4xxxxx
2^(2/2) = 2^1 = 2
2^(3/2) = 2^1.5 = 2.8xxxxx
2^(4/2) = 2^2 = 4
2^(5/2) = 2^2.5 = 5.6xxxxx
2^(6/2) = 2^3 = 8
2^(7/2) = 2^3.5 = 11.3xxxx
2^(8/2) = 2^4 = 16
If anybody is wondering,
2^X means 2 to the power of X.
Quote:
Originally Posted by clevermax  First I took the f-stop as f/2.8, which is precisely 2.8284. |
I took F/2.8 as 2^3/2 or 2^1.5, infinitely accurate. But that's not what is making the difference.
Quote:
Originally Posted by clevermax  1/3rd loss in f-stop will be 2.8284 - (2.8284-2)/3 = 2.5538 |
This is why we are getting different values.
You are dividing the f-stop difference (2.0 to 2.8284) into 3 equal parts. But f-stops are not linear!
Accurate 1/3 f-stop are the following:
2^(0/2)/3 = 2^0/6 = 1
2^(1/2)/3 = 2^1/6
2^(2/2)/3 = 2^2/6
2^(3/2)/3 = 2^3/6 = 1.4xxxx
2^(4/2)/3 = 2^4/6
2^(5/2)/3 = 2^5/6
2^(6/2)/3 = 2^6/6 = 2
2^(7/2)/3 = 2^7/6
2^(8/2)/3 = 2^8/6 <--------------My 1/3 difference (2.5198)
2^(9/2)/3 = 2^9/6 = 2.8xxxx
2^(10/2)/3 = 2^10/6
2^(11/2)/3 = 2^11/6
2^(12/2)/3 = 2^12/6 = 4
2^(13/2)/3 = 2^13/6
2^(14/2)/3 = 2^14/6
2^(15/2)/3 = 2^15/6 = 5.6xxxx
2^(16/2)/3 = 2^16/6
2^(17/2)/3 = 2^17/6
2^(18/2)/3 = 2^18/6 = 8
Consider the following image I just drew:
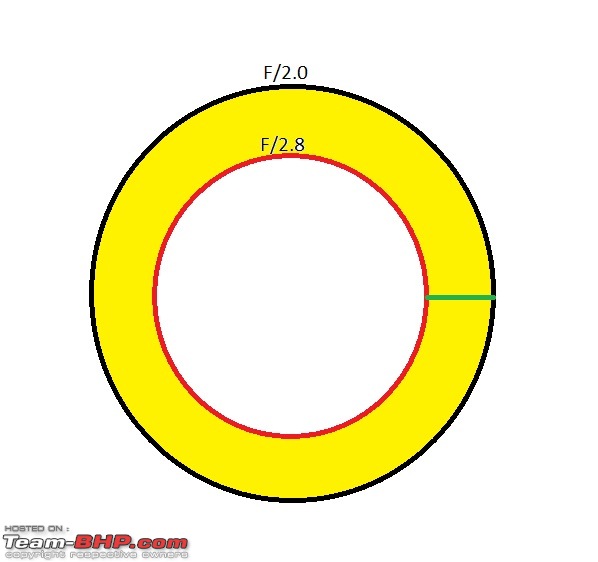
You are dividing the green line into 3 equal parts, I am dividing the the area of yellow portion into 3 equal parts. Considering light is directly proportional to area, isn't my method correct?
Rest of our calculation are same, but the difference in result is coming from the dividing philosophy.
Quote:
Originally Posted by R2D2  |
Even this table is dividing the green line into 10 equal parts, instead of the area of yellow portion.
Mathematically my method is right. But what is the convention used in photography, may not be the same?
Quote:
Originally Posted by R2D2  F1 = 50mm, d=50mm r=25 mm
F1.11 (3 stops down i.e. 1/3rds of a full stop) - d= 45.05mm, r=22.52
Therefore:
Area of aperture @ F1 = 1962.50 sq.mm
Area of aperture @ F1.1 (1/3rd stop less) = 1592.45 sq mm
Drop in area of aperture = 370.05 sq mm which is 18.85% less area and all other things being equal, that %age less light being transmitted |
Ok, let's take this example.
Area of aperture @ F1 = PI X 25 X 25 = 1963.50 sq.mm
Radius @ F1.122462 (1/3rd stop less using my method = 2^1/6) = 22.2724mm
Area of aperture @ F1.122462 = PI X 22.2724 X 22.2724 = 1558.42 sq.mm
Loss in light = (1963.50 - 1558.42)/1963.50 = .206 or 20.6%
So it is consistent.















 here's how, taking a 50mm lens as an example (this works regardless of FL of lens) :
here's how, taking a 50mm lens as an example (this works regardless of FL of lens) :
 .
.