Team-BHP (https://www.team-bhp.com/forum/)

-   Gadgets, Computers & Software (https://www.team-bhp.com/forum/gadgets-computers-software/)

-   -   The DSLR Thread (https://www.team-bhp.com/forum/gadgets-computers-software/11582-dslr-thread-677.html)

Don't forget it doesn't vary linearly but to the square. There was a problem with my calculation, I forgot to square, here is the correct one.

1 stop down is is 50% loss of light
1/2 stop down is 29.3% loss of light
1/3 stop down is 20.6% loss of light (loss due to SLT mirror)

Calculations for 1/3 loss:

F/2.8 = 2^3×0.5 or 2^9/3x0.5 ------------ 3 = 9/3
F/2.5 = 2^8/3x0.5 -----------------1/3 stop less is 8/3

Loss of light (area) = (square of 2.8 - square of 2.51) / square of 2.8 = (8 - 6.35 )/8 = .206 or 20.6%

That's what I thought too, linear. But Samurai is right. Check his calculation below, it is to the square and is ~20% not ~16% per my second post on this topic.

Yes it is to the square. I did some reading afterwards on the 'net. You're dead on. Thanks! :thumbs up

After my first calculation, I too was dubious of my answer. When I noticed 12.25% almost 1/4 of 1 stop loss, I knew I had goofed somewhere. So I went back to basics, amount of light is directly proportional to area, and area is proportional to square of f-stop numbers. Bingo! After some scribbling with paper and pen, I got the right number.:)

Should we expect the iSee in the forthcoming years...:)

That's a good one - iSee! You ought to patent it. :)

With the new man Tim Cook in charge, you never know where Apple will go. Especially if/when the craze for the iPhone plateaus.

Thanks for the exact formula Samurai! But I think the loss in light is 18.57%.

I took more than one examples by picking a random (full)f-stop and did the calculation.

The full f-stops are here for reference:
1.4142
2
2.8284
4
5.6568
8
11.3137
16
22.6274
32
and so on.

First I took the f-stop as f/2.8, which is precisely 2.8284.

1/3rd loss in f-stop will be 2.8284 - (2.8284-2)/3 = 2.5538
Now doing the same calculation as Samurai did (I also derived the same formula out)

(2.8284^2 - 2.5538^2)/2.8284^2 = 18.56%

Taking the f-stop as f/8 now:
1/3rd loss in f-stop will be 8 - (8-5.6568)/3 = 7.2189

Same formula gives
(8^2 - 7.2189^2)/8^2 = 18.57%

Now taking f-stop as f/16

1/3rd loss in f-stop will be 16 - (16-11.3137)/3 = 14.4379

Applying the formula again
(16^2 - 14.4379^2)/16^2 = 18.57%

Guys,

I want to share my experience with a camera flash purchase from overseas.

Recently ordered Yongnuo YN 468 II for canon via ebay.com for Rs.5200/- and selected standard Internation post. After 15 days postman arrived with parcel and asked Rs.2934/- as customs duty (Chennai)!!! Please note that product costs 94USD only . But customs duty 52 USD. The seller informed me that he can not help me in this matter. Then I have paid the duty and collected the parcel. Be careful with overseas purchase. If are not lucky enough, you will get screwed.

Samurai/CM I know we are splitting hairs. LOL!

I just discovered this VERY handy table @ Photographic Tables, for F/stop, Shutter Speed, ISO and EV in Photography

If I use this table that denotes 1/10th of a stop increments -

I get 18.85. :D here's how, taking a 50mm lens as an example (this works regardless of FL of lens) :

F1 = 50mm, d=50mm r=25 mm
F1.11 (3 stops down i.e. 1/3rds of a full stop) - d= 45.05mm, r=22.52

Therefore:

Area of aperture @ F1 = 1962.50 sq.mm
Area of aperture @ F1.1 (1/3rd stop less) = 1592.45 sq mm

Drop in area of aperture = 370.05 sq mm which is 18.85% less area and all other things being equal, that %age less light being transmitted

This is not unknown mate and many people are in for a surprise.

Fact is that any item purchased on the 'net and shipped to India via Courier or Post will be subject to Customs duties. They apply 25%+10%CVD+surcharges which comes to approx 30-33% of cost of the item PLUS the postal/courier charges i.e. CIF.

Always assume you will be charged Customs and then total up the cost of the article. Only place the order if the total cost i.e. cost of flash + shipping + Customs duty is acceptable to you.

Ok, now I am more confused. We are using different methods to divide, but which is right?

I know why you are getting a different result.

My numbers were even more accurate, I didn't stop at 4th decimal. I used the following fractions as my f-stops:

2^(0/2) = 2^0 = 1
2^(1/2) = 2^0.5 = 1.4xxxxx
2^(2/2) = 2^1 = 2
2^(3/2) = 2^1.5 = 2.8xxxxx
2^(4/2) = 2^2 = 4
2^(5/2) = 2^2.5 = 5.6xxxxx
2^(6/2) = 2^3 = 8
2^(7/2) = 2^3.5 = 11.3xxxx
2^(8/2) = 2^4 = 16

If anybody is wondering, 2^X means 2 to the power of X.

I took F/2.8 as 2^3/2 or 2^1.5, infinitely accurate. But that's not what is making the difference.

This is why we are getting different values.

You are dividing the f-stop difference (2.0 to 2.8284) into 3 equal parts. But f-stops are not linear!

Accurate 1/3 f-stop are the following:

2^(0/2)/3 = 2^0/6 = 1
2^(1/2)/3 = 2^1/6
2^(2/2)/3 = 2^2/6
2^(3/2)/3 = 2^3/6 = 1.4xxxx
2^(4/2)/3 = 2^4/6
2^(5/2)/3 = 2^5/6
2^(6/2)/3 = 2^6/6 = 2
2^(7/2)/3 = 2^7/6
2^(8/2)/3 = 2^8/6 <--------------My 1/3 difference (2.5198)
2^(9/2)/3 = 2^9/6 = 2.8xxxx
2^(10/2)/3 = 2^10/6
2^(11/2)/3 = 2^11/6
2^(12/2)/3 = 2^12/6 = 4
2^(13/2)/3 = 2^13/6
2^(14/2)/3 = 2^14/6
2^(15/2)/3 = 2^15/6 = 5.6xxxx
2^(16/2)/3 = 2^16/6
2^(17/2)/3 = 2^17/6
2^(18/2)/3 = 2^18/6 = 8

Consider the following image I just drew:



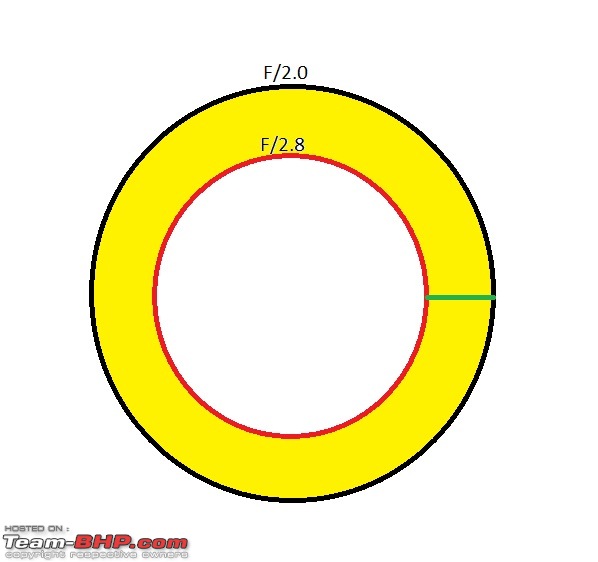
You are dividing the green line into 3 equal parts, I am dividing the the area of yellow portion into 3 equal parts. Considering light is directly proportional to area, isn't my method correct?

Rest of our calculation are same, but the difference in result is coming from the dividing philosophy.

Even this table is dividing the green line into 10 equal parts, instead of the area of yellow portion.

Mathematically my method is right. But what is the convention used in photography, may not be the same?

Ok, let's take this example.

Area of aperture @ F1 = PI X 25 X 25 = 1963.50 sq.mm
Radius @ F1.122462 (1/3rd stop less using my method = 2^1/6) = 22.2724mm
Area of aperture @ F1.122462 = PI X 22.2724 X 22.2724 = 1558.42 sq.mm

Loss in light = (1963.50 - 1558.42)/1963.50 = .206 or 20.6%

So it is consistent.

My brother is a professional cinematographer and we have a 5D Mark II, 7D and a 60D. I am looking to buy a 24-105mm lens and also need a 70-200 or a 75-300 lens. Please suggest if I need a f2.8 or f4 and their usage. of course i know f2.8 is superior than f4 but I am just looking to find what suits my need. What else would I need to complete my package of lens for semi-pro photography as hobby ? apart from 24-105, i need a lens that covers the rest of the range till 200mm or more. Also, image stabilizer is a must. kindly do post in your suggestions and thoughts about it. I could have asked my bro easily but he is out there very busy and unable to have a chat with him :Frustrati .

thanks,
Chaos

Samurai, perfect. I got my mistake, divided fstop value into three, but which cannot be linear. Your method of dividing the area into three equal parts is right.

Quite a learning for me, the whole discussion! Thanks Samurai, R2D2.

There is another way to confirm the number.

Drop of one full stop will result in half light of original or 0.5 amount of light.

Drop of 3 consecutive 1/3 stop should be same as 1 full stop, that is 0.5 amount of light.

If drop due to 1/3 stop is .206, then the light left is 1 - 0.206 = 0.794

So after three consecutive 1/3 stops we will have 0.794 X 0.794 X 0.794 = 0.5 :)

I would suggest you to go for the f/2.8. It will give you a faster lens to play around. Tomorrow, as you progress, you shall not regret this purchase.

Having said that, the 24~105 (Canon EF 24-105mm f/4 L IS USM) is a f/4.

This EF 24-70mm f/2.8L II USM is a f/2.8 and a great lens. Both the above lenses are L series.

If you buy the 24~105 then I would suggest the EF 100-400mm f/4.5-5.6L IS USM and this should cover your range & requirement.

You could also consider the EF 100-300mm f/4.5-5.6 USM that is less than half the price of a 100~400. The f stop for both the lenses is the same except that the latter is a L series.

Hope I haven't confused you much.

This was real funny. You could've left a message on a paper in his room. No? :D

Ditto, thanks Samurai and CM

You were spot on mate. Cheers! :thumbs up,

Knowing how incredibly complex optics are to design and manufacture I believe they'd be using the calculations you outlined i.e. to the root, not linear. Every bit of accuracy helps.

After reading around quite a bit on optics (nearly all of which went over my head) here's an XLS I created with calculations for 1/3, 1/2 and full stop incremements using a hypothetical 50mm prime lens. And yes it is a 20.63% drop over 1/3rd stop. Hope people participating on this thread find the XLS useful.

After some research I have now decided to go ahead with the purchase of Nikon D7000. Now, I need advice on getting best deal for this Camera. I checked out Flipkart and their's is the best price at Rs. 57666. But, currently they are out of stock. Ezone online is also quoting the same price but I don't know how genuine they are. Do I have any other options?