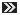| | #4141 |
| Newbie Join Date: Aug 2015 Location: Gurgaon
Posts: 20
Thanked: 218 Times
| |
| |
| |
| | #4142 |
| BHPian | |
| |
| | #4143 |
| Senior - BHPian | |
| |  (1)
Thanks (1)
Thanks
|
| | #4144 |
| BHPian | |
| |
| | #4145 |
| Senior - BHPian | |
| |  (1)
Thanks (1)
Thanks
|
| | #4146 |
| Senior - BHPian | |
| |
| | #4147 |
| Newbie Join Date: Aug 2015 Location: Gurgaon
Posts: 20
Thanked: 218 Times
| |
| |  (1)
Thanks (1)
Thanks
|
| | #4148 |
| BHPian | |
| |  (1)
Thanks (1)
Thanks
|
| | #4149 |
| BHPian Join Date: Dec 2016 Location: Pune
Posts: 213
Thanked: 1,023 Times
| |
| |  (1)
Thanks (1)
Thanks
|
| | #4150 |
| Senior - BHPian | |
| |  (1)
Thanks (1)
Thanks
|
| | #4151 |
| BHPian Join Date: Apr 2017 Location: Bangalore
Posts: 31
Thanked: 9 Times
| |
| |
| |
| | #4152 |
| BHPian | |
| |
| | #4153 |
| Senior - BHPian | |
| |
| | #4154 |
| BHPian Join Date: May 2017 Location: Pune
Posts: 148
Thanked: 401 Times
| |
| |
| | #4155 |
| Senior - BHPian | |
| |  (2)
Thanks (2)
Thanks
|
 |
Most Viewed